Tag: frontpage

La (non)fotocopiatrice quantistica

by Carlo_Nicolini • 19 Novembre 2008 • 0 Comments

Discorso immaginario fra un impiegato del futuro ed un tecnico di fotocopiatrici:

Impiegato: Buongiorno, ho un problema con la vostra macchina.

Tecnico: Mi dica.

Impiegato: Quando metto un foglio nella fotocopiatrice e premo copia l’originale scompare! Fra l’altro la copia finale è orrenda!

Tecnico: E’ normale.

Impiegato: Ma la vostra fotocopiatrice è inutile allora!

Tecnico: L’ha deciso lei di comprare una fotocopiatrice quantistica…

Ok, lo ammetto. Tutto ciò sarebbe impossibile, però è bello immaginarlo.

Perché il povero impiegato non ha motivo di lamentarsi con il tecnico?

Ovviamente una fotocopiatrice quantistica non potrebbe esistere per il semplice fatto che distruggerebbe il ben noto principio di indeterminazione, infatti sarebbe possibile “clonare” un sistema in diverse copie identiche e poi ad esempio per ogni coppia di copie misurare osservabili coniugate come posizione ed impulso, venendole a conoscere contemporaneamente senza introdurre indeterminazioni nella misura.

Tutto ciò non è possibile, la meccanica quantistica così com’è sparirebbe, infatti un meccanismo del genere trascenderebbe la linearità dell’equazione di Schroedinger (vedi Wooters [1982])

Analizziamo la questione dal punto di vista della meccanica quantistica.

Supponiamo che il nostro documento sia rappresentato da una funzione d’onda $\left | \psi \right>$ e che il foglio bianco sia descrivibile mediante $\left | X \right>$ .

Il nostro dispositivo replicatore dovrebbe comportarsi in modo da replicare lo stato $\left | \psi \right>$ sullo stato $\left | X \right>$ .

Quello che vogliamo ottenere è un processo del genere:

$\left | \psi \right> \left | X \right> \rightarrow \left | \psi \right>\left | \psi \right>$

Quindi per due generici stati ortogonali $\left | \psi_1 \right> , \left | \psi_2 \right>$ avremo che il sistema si comporterà nella seguente maniera:

$\left | \psi_1 \right> \left | X \right> \rightarrow \left | \psi_1 \right>\left | \psi_1 \right>$

$\left | \psi_2 \right> \left | X \right> \rightarrow \left | \psi_2 \right>\left | \psi_2 \right>$

Fin qui nessun problema, sembra che tutto funzioni. Ma se invece di stati puri, mandiamo stati miscela ossia combinazioni lineari di stati puri?

Ci aspetteremo che per uno stato sovrapposizione lineare di due autostati del tipo $\left | \phi \right> = \alpha \left | \psi_1 \right> + \beta \left | \psi_2 \right>$ il sistema dovrebbe fornire un comportamento del genere:

Invece (fatevi due conticini) quello che succede è questo:

$\left | \phi \right> \left | X \right> \rightarrow \alpha^2 \left | \psi_1 \right> \left | \psi_1 \right> + \beta^2 \left | \psi_2 \right> \left | \psi_2 \right> + \alpha \beta \left \{ \left | \psi_1 \right> \left | \psi_2 \right> \right + \left | \psi_2 \right> \left | \psi_1 \right>\}$

Cosa significa tutto ciò?

Semplice, è come avere una fotocopiatrice che copia correttamente solo le righe orizzontali e verticali, distorcendo invece le diagonali.

Questi argomenti sembrano un po’ complessi ma in realtà questa spiegazione è molto semplice e soprattutto attuale. Gli sviluppi recenti della crittografia quantistica si basano infatti su questi asserti.

Referenze

J.Griffith – Introduzione alla meccanica quantistica

Wooters, Zureck, Nature 299, 802 (1982

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

La pentola guardata non bolle mai

by Carlo_Nicolini • 10 Novembre 2008 • 0 Comments

Per i precisi, “l’acqua contenuta in una pentola posta sul fuoco e troppo guardata non bolle mai”.

Penso poi che sia possibile applicare questa considerazione anche alla moka del caffè, per analogia di fisica coinvolta 🙂

L’avete capito bene, l’argomento di oggi è il paradosso di Zenone quantistico che in realtà è stato chiamato da qualche mattacchione ¹ “paradosso della pentola troppo guardata”.

Ma torniamo alla fisica vera e alla meccanica quantistica. Questo effetto ci dimostra che, grazie a quello strano concetto che va sotto il nome di “collasso della funzione d’onda” un sistema quantistico la cui naturale evoluzione sarebbe una transizione da uno stato ad un altro, se posto con contitinuità ad un processo di misurazione, resta immutato.

Questo argomento può assomigliare al famoso paradosso della freccia di Zenone di Elea, il filosofo greco, che tentava di dimostrare come il movimento non possa in effetti esistere.

L’argomento di Zenone era quello della freccia, che scagliata dall’arciere verso un bersaglio doveva percorrere infiniti tratti sempre più brevi senza mai, di fatto, arrivare a destinazione: il moto è impossibile!

Ma analizziamo la questione quantistica:

Abbiamo un atomo in uno stato eccitato, instabile e lo sottoponiamo ad una serie di misurazioni ripetute nel tempo. Ogni osservazione causa il collasso della funzione d’onda, “azzerando il conto alla rovescia” e permettendo a quello stato di permanere indefinitamente.

Osservazione significa per il fisico, invio di fotoni, energia che permetta di conoscere una volta ritornata al mittente la situazione. Abbiamo a che fare quindi con un esempio di interazione radiazione materia. Si dimostra che la probabilità di transizione di un sistema illuminato da una radiazione incoerente dipende linearmente dal tempo per cui questa radiazione è “accesa”.

Dal momento che la velocità di transizione è 1/tau allora

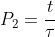
$P_2=\frac{t}{\tau}$

se il sistema è a due livelli, la probabilità che il sistema sia ancora nello stato eccitato dopo un tempo t è

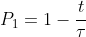
$P_1=1-\frac{t}{\tau}$

Se la misurazione ci informa ancora che il sistema è nello stato eccitato allora significa che la funzione d’onda è nuovamente collassata allo stato eccitato e quindi il processo ricomincia.

Misurando il sistema ad un tempo 2t la probabilità che sia nello stato eccitato sarà chiaramente:

$P_2=\left(1-\frac{t}{\tau}\right)^2 \approx 1-2 \frac{t}{\tau}$

sviluppato per t piccolo,cioè lo stesso andamento in termini di probabilità che avremmo se non avessimo fatto alcuna misura all’istante t.

Quando i tempi di osservazione si riducono molto rispetto al tempo di vita medio dello stato 2, si dimostra che la probabilità di transizione è proporzionale a 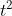$t^2$ anziché a $t$ .

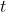In questo caso allora lo sviluppo relativo all’osservazione all’istante 2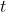 $t$ causerà una probabilità che il sistema si trovi ancora nello stato superiore proporzionale a 2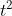 $t^2$

$P_2 \propto 1- 2t^2$

mentre se non avessimo fatto alcuna misura sarebbe stata semplicemente

$P_2 \propto 1- 4t^2$

Estendendo il ragionamento a 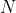$N$ osservazioni distanziate ad intervalli regolari 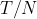$T/N$ (dove T è il tempo totale di osservazione) abbiamo che nel limite di infinite osservazioni (leggi continuo) la probabilità di trovare il sistema nello stato eccitato è 1 ovvero l’evento certo!

Un sistema osservato continuamente non decade mai!

Come è possibile allora il tracciamento delle particelle nelle camere a bolle?

Il processo di misurazione è davvero così invasivo? Il collasso della funzione d’onda è una bufala messa in piedi per fare tornare i conti e tutto che quello che mi hai detto finora son fregnacce?

Non penso. Il concetto di collasso della funzione d’onda, sebbene sia così difficile da intuire riesce a chiarire diversi concetti. Ritengo che i sostenitori di interpretazioni della meccanica quantistica che supportano teorie in cui è necessario l’intervento dell’osservatore (umano) esterno oppure in cui è tirato in ballo il processo di coscienza (interpretazione a molte menti) stiano semplicemente cercando di portare a livello di intuizione qualcosa che di per sé non è nato per farsi comprendere in termini semplici.

Ricordiamoci che la natura e le sue leggi non sono state modellate in base a quell’equazione o a quell’altra e che quello che conosciamo fino ad ora è solo un modello che sarà necessariamente incompleto. I fenomeni naturali non hanno bisogno dell’osservazione dell’essere umano per manifestarsi. Per Wigner ad esempio la funzione d’onda collassa nel momento in cui l’informazione giunge al cervello dell’osservatore. Con che pretesa Wigner suppone che la mente umana, che altro non è composta che di materia ordinaria, si possa porre su un gradino superiore (ovviamente non dal punto di vista funzionale) ad un qualsiasi atomo dell’universo? Una buona teoria deve essere quanto più possibile oggettiva ma soprattutto un’interpretazione simile sposta il piano di analisi ad un livello in cui l’analisi non è possibile!

Il collasso della funzione d’onda è qualcosa di più sottile dunque di un semplice processo di presa di coscienza e da quanto si sa ora, il migliore approccio resta sempre quello della scuola di Copenhagen. Questo ovviamente non esclude nessuna possibile nuova teoria ma di sicuro se è stata l’interpretazione che ha portato la maggioranza dei risultati, è difficile che possa venire smontata da un giorno all’altro. Benvengano sempre le nuove idee, a patto che siano capaci di spiegare razionalmente qualcosa che alle idee precedenti sfuggiva

Questo non esclude che le domande sul collasso della funzione d’onda restino ancora aperte, ma fortunatamente certe interpretazioni che fanno riferimento a variabili nascoste siano state eliminate.

Torniamo all’effetto Zenone. Il mantenenimento della funzione d’onda collassata blocca l’evoluzione della stessa!

Potrete contraddirmi affermando che il tracciamento di una particella in un rivelatore, sia un processo di misura ripetuto in continuo e che quindi un pione, dotato di una certa vita media, se tracciato in una camera a bolle non debba mai decadere. Avete dunque intuito la natura del paradosso di Zenone quantistico.

Prima di tutto puntualizziamo che in un processo di interazione simile non è possibile non comprendere il sistema particella+rivelatore nella sua interezza. In secondo luogo, la particella interagisce solo “ad intermittenza” con le altre particella che costituiscono il rivelatore. Bisogna notare inoltre che per l’apparire del fenomeno il sistema deve essere tenuto osservato nel regime di dipendenza da 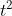$t^2$ e questo è possibile solo se le interazioni sono estremamente ravvicinate.

Dimostrare quindi l’effetto Zenone quantistico è di fatto impossibile per transizioni spontaneee come i decadimenti ma si è reso sperimentalmente fattibile per transizioni indotte (eccitazioni con laser di sistemi preparati in uno stato).

Referenze

Greiner, Quantum Mechanics, An introduction. Springer (2001)

Bell, Speakable and unspeakable in quantum mechanics.

J.Griffith – Introduzione alla meccanica quantistica.

Note:

1 George Sudarshan and Baidyanaith Misra ,1977

{jumi [adsense/adsense468x15.html]}

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

La pentola guardata non bolle mai

by Carlo_Nicolini • 10 Novembre 2008 • Commenti disabilitati

Per i precisi, “l’acqua contenuta in una pentola posta sul fuoco e troppo guardata non bolle mai”.

Penso poi che sia possibile applicare questa considerazione anche alla moka del caffè, per analogia di fisica coinvolta 🙂

L’avete capito bene, l’argomento di oggi è il paradosso di Zenone quantistico che in realtà è stato chiamato da qualche mattacchione ¹ “paradosso della pentola troppo guardata”.

Questo argomento può assomigliare al famoso paradosso della freccia di Zenone di Elea, il filosofo greco, che tentava di dimostrare come il movimento non possa in effetti esistere.

Ma analizziamo la questione quantistica:

Dal momento che la velocità di transizione è 1/tau allora

$P_2=\frac{t}{\tau}$

se il sistema è a due livelli, la probabilità che il sistema sia ancora nello stato eccitato dopo un tempo t è

$P_1=1-\frac{t}{\tau}$

Se la misurazione ci informa ancora che il sistema è nello stato eccitato allora significa che la funzione d’onda è nuovamente collassata allo stato eccitato e quindi il processo ricomincia.

Misurando il sistema ad un tempo 2t la probabilità che sia nello stato eccitato sarà chiaramente:

$P_2=\left(1-\frac{t}{\tau}\right)^2 \approx 1-2 \frac{t}{\tau}$

sviluppato per t piccolo,cioè lo stesso andamento in termini di probabilità che avremmo se non avessimo fatto alcuna misura all’istante t.

Quando i tempi di osservazione si riducono molto rispetto al tempo di vita medio dello stato 2, si dimostra che la probabilità di transizione è proporzionale a $t^2$ anziché a $t$ .

In questo caso allora lo sviluppo relativo all’osservazione all’istante 2 $t$ causerà una probabilità che il sistema si trovi ancora nello stato superiore proporzionale a 2 $t^2$

$P_2 \propto 1- 2t^2$

mentre se non avessimo fatto alcuna misura sarebbe stata semplicemente

$P_2 \propto 1- 4t^2$

Un sistema osservato continuamente non decade mai!

Come è possibile allora il tracciamento delle particelle nelle camere a bolle?

Questo non esclude che le domande sul collasso della funzione d’onda restino ancora aperte, ma fortunatamente certe interpretazioni che fanno riferimento a variabili nascoste siano state eliminate.

Torniamo all’effetto Zenone. Il mantenenimento della funzione d’onda collassata blocca l’evoluzione della stessa!

Referenze

Greiner, Quantum Mechanics, An introduction. Springer (2001)

Bell, Speakable and unspeakable in quantum mechanics.

J.Griffith – Introduzione alla meccanica quantistica.

Note:

1 George Sudarshan and Baidyanaith Misra ,1977

{jumi [adsense/adsense468x15.html]}

Puoi leggere l\’Articolo completo direttamente sul sito di Home

Parliamo dell’effetto Ahronov-Bohm

by Carlo_Nicolini • 27 Ottobre 2008 • 0 Comments

Come no, tutti lo conoscono!

L’effetto Ahronov-Bohm, eponimo dei suoi scopritori, è un effetto quantistico che si manifesta come un “azione” dei potenziali sulle particelle cariche anche dove i campi sono nulli.

L’esperimento che mostra questo effetto è il seguente:

Consideriamo un pennello di elettroni che sia separato in due fasci divisi. I due fasci elettronici in assenza di elementi posti dietro alle fenditure creeranno delle figure di interferenza (diffrazione di elettroni) mostrando dei picchi.

Se ora poniamo dietro le aperture un solenoide in cui sia fatta fluire corrente distante dai percorsi dei due fasci, nonostante gli elettroni non attraversino le linee di campo magnetico che risultano confinate solamente all’interno del solenoide, la figura di interferenza subirà un cambiamento.

Setup sperimentale. La zona B è la zona in cui è presente il campo magnetico (un solenoide).

Com’è possibile ciò? Gli elettroni, in quanto particelle cariche, non risentono della forza di Lorentz? Se B=0 allora anche la forza di Lorentz sarà nulla!

In realtà le particelle quantistiche non interagiscono con il campo magnetico ma con il potenziale vettore di questo campo, A, $\mathbf{B}=\nabla \times \mathbf{A}$ , quindi in qualche modo lo “sfuggente” potenziale vettore influenza la fase dell’elettrone.

Si dimostra, partendo dalla sostituzione minimale nell’equazione di Schroedinger, che la fase accumulata nel percorso dell’elettrone è fornita da

creando una differenza di fase fra due percorsi data dall’interessante formula

Quest’ultima equazione coinvolge il flusso del campo magnetico (calcolato con il teorema di Stokes) attraverso l’area compresa fra i due percorsi.

Ma ora viene da chiedersi come sia possibile l’interazione fra particella e potenziale vettore A.

La trattazione rigorosa prevede lo studio dell’equazione di Schroedinger in presenza di campo elettromagnetico e lo studio della sua invarianza di gauge, tuttavia qualcosa sfugge ancora alla piena comprensione del fenomeno.

Questi studi hanno portato Bohm a formulare un’interpretazione ontologica della meccanica quantistica.

Molto brevemente, i punti principali di questa interpretazione possono essere riassunti a partire da alcune considerazione sull’equazione di Schrodinger. Riscrivendo la funzione d’onda in forma polare

$\psi = R \exp{(iS/h)}$

l’equazione di Schrodinger in presenza di un potenziale V assume la forma di due equazioni per il modulo R e la fase S/h della funzione d’onda:

$\begin{array}{l} \frac{{\partial S}}{{\partial t}} + \frac{{\left( {\nabla S} \right)^2 }}{{2m}} + V - \frac{{\hbar ^2 }}{{2m}}\frac{{\nabla ^2 R}}{R} = 0 \\ \frac{{\partial R^2 }}{{\partial t}} + \nabla \cdot \left( {R^2 \frac{{\nabla S}}{m}} \right) = 0 \\ \end{array}$

La prima equazione nel limite h->0 (limite classico) restituisce le equazioni di Hamilton Jacobi (qundi il moto classico-deterministico) mentre la seconda, più interessante si può leggere come una conservazione della probabilità in un “ensemble” di particelle, aventi un movimento normale allo stesso fronte d’onda con una densità di probabilità $P=R^2$ dove R è l’ampiezza della funzione d’onda (modulo).

Qui sembra emergere la descrizione di particella che conosciamo nella vita di tutti i giorni, senza tutte le ambiguità della meccanica quantistica, principi di indeterminazione, collasso della funzione d’onda etc.

Una particella alla quale `e stata attribuita una “realtà” oggettiva, cioè un corpo mareriale di una certa massa, carica e momento che descrive una traiettoria visualizzabile come una successione causale di punti nello spazio.

Che la visione classica ontologica non si possa estendere al dominio quantistico grazie a questa interpretazione? Ovvero, le equazioni di Hamilton Jacobi possono essere estese alla meccanica quantistica con l’aggiunta di un nuovo termine, detto potenziale quantistico?

Il potenziale quantistico si comporta da tramite per trasportare informazione, come una sorta di onda pilota? Attraverso questa nuova nozione, è possibile interpretare l’esperimento di interferenza dicendo che gli elettroni hanno l’abilità di compiere lavoro sotto l’influenza dell’informazione attiva descritta dal campo quantistico.

Il problema che noto io è che la teoria delle onde pilota si pone come una teoria a variabile nascosta (in questo caso il potenziale quantistico) e proprio Bell ha confermato grazie al suo teorema che le teoria a variabile nascosta sono incompatibili con le predizioni della meccanica quantistica.

http://it.wikipedia.org/wiki/Teorema_di_Bell

Referenze:

J.Griffith – Introduzione alla meccanica quantistica.

Schiff – Quantum Mechanics

Cristiano Fidani – L’effetto ahronov Bohm e il potenziale quantistico. http://ulisse.sissa.it/biblioteca/saggio/2007/Ubib070622s001

http://en.wikipedia.org/wiki/Aharonov-Bohm_effect

P.S.Un’implicazione è inoltre la quantizzazione del flusso di campo magnetico in multipli di $\hbar /2e$ .

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

Problema conciso

by Carlo_Nicolini • 13 Ottobre 2008 • 0 Comments

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini Pages – Home

Bilance e scatole

by Carlo_Nicolini • 8 Ottobre 2008 • 0 Comments

Siamo in una prigione dove gli aguzzini si divertono a porci tranelli per prendersi gioco di noi.

L’aguzzino ci propone un enigma:

Abbiamo dieci scatole, contenenti ognuna 10 pezzi di pane. 9 Pezzi di pane pesano 100 gr, uno di questi 10 pezzi invece pesa 105 gr.

Possiamo avere il nostro pasto solamente se con una sola pesata a disposizione siamo capaci di determinare quale scatola contiene il pezzo da 105 gr.

Maledetti aguzzini…cosa diciamo?

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini Pages – Home

Dave Hill

by Carlo_Nicolini • 7 Ottobre 2008 • 0 Comments

Un tutorial per creare immagini a metà fra illustrazione e fotografia. La tecnica è quella del fotografo Dave Hill.http://www.davehillphoto.com/Apriamo un’immagine, duplichiamo il livello.Ora scegliamo Filtro->Altri->Passa Alto. Inseriamo il va…

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

Matrice CKM

by Carlo_Nicolini • 7 Ottobre 2008 • 0 Comments

E’ notizia di questi giorni l’assegnazione del premio Nobel per la fisica ai tre fisici giapponesi Yoichiro Nambu¹, Makoto Kobayashi e Toshihide Maskawa per scoperte nell’ambito della fisica nucleare.

Queste scoperte sono state ispirate però da un articolo apparso nel 1963 (Phys.Rev.Lett. 10 (1963) 531 ) ad opera dell’italiano Nicola Cabibbo. La scoperta dell’italiano è stata l’interpretazione di alcuni processi di trasformazione di quark (mescolamento). Quest’interpretazione, risalente al 1963, quando il concetto di quark non era stato ancora introdotto, tratta in termini algebrici le probabilità di transizione fra tipi di quark²

Più semplicemente possibile, cosa significa?

Parliamo in termini più moderni: possiamo raggruppare le 3 famiglie di quark, ovvero le particelle elementari fermioniche di carica frazionaria, secondo le loro cariche e masse,

$\begin{pmatrix} u \\d \end{pmatrix} \begin{pmatrix} c \\s \end{pmatrix} \begin{pmatrix} t \\b \end{pmatrix}$

dove le sigle u,d,c,s,t,b stanno rispettivamente per Up, Down, Charme, Strange, Top, Bottom e rappresentano le 6 tipologie di quark conosciuti.

In interazioni deboli con scambio di correnti cariche, il “partner” di un autostato di “sapore” $\left|d \right>$ non è soltanto l’autostato $\left|u \right>$ ma piuttosto una combinazione lineare del tipo:

$\left|d' \right> = \alpha_1 \left|u \right> + \alpha_2 \left|s \right>$

Uno dei meriti di Cabibbo è stato capire che il mixing, ovvero la transizione da un quark q ad un quark q’ è descrivibile mediante una matrice di rotazione, infatti i coefficienti che compaiono nelle combinazioni lineari $\alpha_1,\alpha_2$ possono essere scritti come il seno ed il coseno di un angolo $\theta_C$ detto Angolo di Cabibbo. Quindi la matrice di Cabibbo risulta come:

$\begin{pmatrix} \left| d' \right> \\ \left| s' \right> \end{pmatrix} = \begin{pmatrix} \cos \theta_C & \sin \theta_C \\ -\sin \theta_C & \cos \theta_C \end{pmatrix} \begin{pmatrix} \left| d \right> \\ \left| s \right> \end{pmatrix}$

Cabibbo ha trattato complicati fenomeni descritti negli esperimenti e predetti poi dagli sviluppi della fisica teorica come semplici rotazioni di vettori, grazie al suo articolo breve, coinciso ed efficace.s

Tale matrice, descrivendo di fatto possibilità non nulle di transizione di quark da una famiglia all’altra è importante nello studio della violazione di carica e parità (Violazione CP).

La scoperta per cui sarà assegnato il premio Nobel ai giapponesi Makoto Kobayashi e Toshihide Maskawa è stata la generalizzazione della suddetta matrice alla terza generazione di quark, ovvero Top e Bottom. Similarmente vengono descritte le probabilità di transizione con le probabilità espresse dal modulo quadro degli elementi di matrice coinvolti, ad esempio, la probabilità che in un’interazione debole avvenga una trasformazione da quark q -> q’ sarà data da $\left| V_{qq'} \right|^2$ . Estendendo la matrice di Cabibbo, possiamo parlare di Matrice CKN (Cabibbo, Kobayashi, Maskawa)

I valori numerici dei coefficienti della matrice sono ora conosciuti con una certa precisione grazie a misure sperimentali.

Dopo tutto questo, sembra ovvio capire perchè resta l’amaro in bocca alla scienza italiana. L’incipit di Cabibbo non è stato valutato.

Note

¹ Nambu è stato il primo a proporre la carica “colore” fondando di fatto la cromodinamica quantistica, ovvero lo studio della meccanica quantistica di particelle dotate oltre che di carica di massa e di carica elettrica, anche di una cosiddetta carica di colore (r,g,b). Nambu è stato uno dei fondatori della teoria delle stringhe.

² Simili processi di mixing non sono mai stati osservati per processi leptonici, la conservazione del numero leptonico sembra non essere mai violata. Tale legge di conservazione potrebbe essere confutata qualora venisse misurata diversa da zero la massa del neutrino, ciò comporterebbe che gli autostati neutrinici tau, elettronico, muonico non sarebbero più tali e potrebbe verificarsi la transizione da un tipo all’altro. Alcuni esperimenti in giro per il mondo (laboratori del gran sasso) cercano di verificare l’ipotesi di massività del neutrino, per ora senza nessun risultato.

Referenze

Povh Rith Schelze, Particelle e nuclei, Bollati Boringhieri

N.Cabibbo, Phys.Rev.Lett. 10 (1963) 531

http://it.wikipedia.org/wiki/Matrice_CKM

S.Boffi – Da Laplace ad Heisenberg: un’introduzione alla meccanica quantistica ed alle sue applicazioni. La Goliardica Pavese 1992.

http://prometeo.sif.it:8080/papers/online/sag/024/05-06/pdf/09.pdf

APPENDICE:

Sono mostrati i protagonisti del modello standard della fisica delle particelle. I fermioni, particelle con spin semi-intero, rispondenti alla statistica di Fermi-Dirac sono i quarks ed i leptoni. I fermioni sono i costituenti della materia nelle sue varie formazioni, dai protoni ai neutroni. I fermioni si dividono in quark e leptoni. “Stranamente” quarks e leptoni sono 6 per tipo e raggruppati ognuno con il proprio partner.

I bosoni invece sono le particelle mediatrici delle forze e sono 4: il fotone responsabile dell’interazione elettromagnetica, protagonista delle elettrodinamica quantistica, il gluone, responsabile dell’interazione nucleare forte, quella che tiene insieme i nuclei atomici, portatore di carica di colore e quindi oggetto complesso che fa la sua parte nella complicata cromodinamica quantistica ed infine i due mediatori dell’interazione debole Z⁰ e W^+- per la cui individuazione Carlo Rubbia ricevette il nobel nel 1984 (Mio anno di nascita!)

La scoperta delle classi di quarks è avvenuta di pari passo con la crescente energia disponibile negli acceleratori di particelle.

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

Quesiti ingannevoli

by Carlo_Nicolini • 30 Settembre 2008 • 0 Comments

Il treno A viaggia a 240 Km/h verso il treno B, che a sua volta viaggia verso A a 150Km/h.

Una mosca percorre la distanza tra i due treni a 300Km/h partendo da A e torna indietro non appena raggiunge il treno B, salvo subito invertire nuovamente la marcia e tornare indietro: continua così finché non viene spiaccicata tra i due treni che si scontrano giusto un’ora dopo la partenza della mosca.

Quale distanza ha percorso la mosca?

La soluzione è dietro l’angolo…

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini Pages – Home

Come scattare in HDR

by Carlo_Nicolini • 29 Settembre 2008 • 0 Comments

La maggior parte delle fotocamere digitali sono capaci di catturare solo una parte limitate del range luminoso di un’immagine. Questo è il motivo per cui le immagini HDR sono create partendo da più scatti ognuno con livelli di esposizione diversi.

Esistono alcune raccomandazioni da prendere in considerazione prima di scattare foto a diversi EV.

1. Avvalersi di un treppiede o cavalletto. Facendo così si eviterà che le diverse immagini registrate siano relative ad una scena leggermente spostata.

2. Impostare la fotocamera sulla modalità manuale preferibilmente. Selezionare un’apertura adatta per la propria scena con il più basso livello ISO possibile. Questo accorgimento ridurrà notevolmente il rumore ISO che viene notevolmente accentuato durante la procedura di tone-mapping.

3. Misurare la luce nella zona più luminosa della scena, prenderne nota. Fare lo stesso per le zone di ombre più rilevanti.

4. Determinare il numero ed il valore di esposizioni necessarie a coprire il range dinamico della scena. Moltiplicare il tempo di esposizione per le zone luminose per 4 per trovare la prossima esposizione distante 2 EV. Moltiplicare di nuovo per 4 per aumentare di altri 2 EV.
Normalmente per una scena outdoor alla luce del giorno bastano 3 esposizioni spaziate di 2 EV.

5. Assicurarsi di non aver mosso la fotocamere fra un’esposizione e l’altra. Preferibilmente utilizzare l’autoscatto per evitare i micromossi

6. Se la propria fotocamera lo permette sfruttare la funzione Auto Exposure Bracketing. Le più avanzate reflex permettono anche 7 esposizioni spaziate fino a 2 EV.

Una volta prese le fotografie darle in pasto ad uno dei programmi descritti negli altri articoli.

Puoi leggere l\’Articolo completo direttamente sul sito di Home

I programmi HDR

by Carlo_Nicolini • 29 Settembre 2008 • 0 Comments

Esistono diversi programmi per creare immagini HDR, tuttavia i più famosi (e funzionanti) si contano sulle dita di una mano:

Photomatix: il migliore,manca però la possibilità di scegliere quale algoritmo di tone mapping utilizzare. I risultati tuttavia sono veloci e di alta qualità Questo software tuttavia è molto costoso e magari per togliersi certi sfizi conviene prima guardare i risultati con QtPfsGui.

Adobe Photoshop CS3: celeberrimo programma di fotoritocco. Incorpora anche la possibilità di creare immagini HDR e di eseguire il tonemapping. Sui dettagli fini si comporta meglio di PhotoMatix ma la resa cromatica non è così buona, e siccome con la fotografia HDR si cercano colori particolari consiglio di lavorare successivamente sull’immagine con gli strumenti che questo software di fotoritocco mette a disposizione.

QtPfsGui: progetto open-source, multipiattaforma. Permette la scelta dell’algoritmo di tone mappin. E’ scaricabile la versione completa ed anche il sorgente per chi ci volesse mettere mano.

Puoi leggere l\’Articolo completo direttamente sul sito di Home

I programmi HDR

by Carlo_Nicolini • 29 Settembre 2008 • 0 Comments

Esistono diversi programmi per creare immagini HDR, tuttavia i più famosi (e funzionanti) si contano sulle dita di una mano:

QtPfsGui: progetto open-source, multipiattaforma. Permette la scelta dell’algoritmo di tone mappin. E’ scaricabile la versione completa ed anche il sorgente per chi ci volesse mettere mano.

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini Pages – Home

I programmi HDR

by Carlo_Nicolini • 29 Settembre 2008 • 0 Comments

Esistono diversi programmi per creare immagini HDR, tuttavia i più famosi (e funzionanti) si contano sulle dita di una mano:

QtPfsGui: progetto open-source, multipiattaforma. Permette la scelta dell’algoritmo di tone mappin. E’ scaricabile la versione completa ed anche il sorgente per chi ci volesse mettere mano.

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini Pages – Home

Qualche cenno alla tecnica HDR

by Carlo_Nicolini • 23 Settembre 2008 • Commenti disabilitati

HDR sta per High Dynamic Range imaging, è una tecnica fotografica abbastanza recente.

http://it.wikipedia.org/wiki/High_dynamic_range_imaging

Esistono molti tutorial sulla fotografia in HDR quindi non starò qua a spiegarvi come si fa, vi indico alcuni siti:

http://www.ai-net.it/tecnologia/foto_HDR_fotografia_immagine_creare_hdr.html

Si possono fare foto del genere…

Tuttavia io che non queste grandi capacità di fotografo sono riuscito a fare questi scatti, sul Lago di Garda in una mattina di agosto.

Puoi leggere l\’Articolo completo direttamente sul sito di Home

Le proprietà dell’amido di mais

by Carlo_Nicolini • 23 Settembre 2008 • 0 Comments

La ricetta è facile: dite alla vostra massaia preferita di andarvi a prendere una confezione di amido di mais (quello con la scritta Maizena per intenderci) o anche la fecola di patate, 250 gr.

Preparate una terrina, un cucchiaio ed iniziate a mescolare 125 gr di amido di mais con dell’acqua tiepida, mescolando fino a che la consistenza dell’impasto non sia troppo liquida nè eccessivamente solida. Per capirci quando battete con forza il cucchiaio sull’impasto non parte nessuno schizzo.

Fase 1

Continuate e mescolate anche i restanti 125 gr, mettendo acqua in quantità sufficiente da mantenere le proprietà precedenti.

Fase 2

Ora avete creato un liquido non newtoniano, ovvero un sistema la cui viscosità dipende in maniera non lineare dall’intensità dello sforzo di taglio applicato. Tradotto: se cercate di agitarlo con violenza o imprimete delle forze impulsive il liquido si comporterà quasi come un solido, mentre se cercherete di penetrarlo lentamente, ad esempio con un dito, l’impasto si comporterà come un liquido poco viscoso.

Curva reologica di un liquido non newtoniano

Gli esperimenti che si possono fare con questo impasto sono molteplici, ma forse i più interessanti sono quelli che riguardano le sollecitazioni prodotte prodotte da onde acustiche (preferibilmente pure).

Preparate un cd contenente diverse frequenze sonore pure (onde sinusoidali a partire dai 30 Hz fino ai 150 Hz) e ricoprite un buon subwoofer con un nylon (ho usato il nylon per cucina). Alzate il volume a tutta sperando che il vostro vicino sia sordo e versate il liquido preparato sul woofer.

Fase 3

Inizialmente si creerano delle onde di superficie stazionarie. Ho notato che questo tipo di onde, nonostante il dominio circolare, non creino nodi e ventri rispondenti alla tipica equazione del tamburo vibrante, in breve suppongo che le autofunzioni rappresentate dall’altezza del fluido visibile, appartengano ad una classe di equazioni delle onde con termini di densità fortemente non lineari. I modi normali di questo sistemi NON sono i modi normali della membrana circolare. (come pare anche ovvio in fondo viste le proprietà di questo fluido).

Basti solo considerare che la propagazione ondosa in fluido la cui viscosità dipende dallo sforzo, diventa una funzione non lineare della densità.

Alcuni ricercatori hanno verificato il comportamento reologico di una soluzione di Mazenza 50-50 http://glass.ruc.dk/studentprojects.php .

Fase 4

Oltre una certa soglia di intensità sonora questi modi normali venutisi a creare evolvono in uno stato disordinato, acquisendo la terza dimensione e creando così particolari modi di vibrazioni tridimensionali, vale a dire, delle specie di mostricciattoli che si muovono sul vostro subwoofer.

L’evoluzione dello stato del sistema dipende dal tempo, le onde stazionarie scompaiono ed assistiamo a strani fenomeni, come quello documentato qua sotto e nella figura precedente.

Fase 5

P.S. Fate questi esperimenti quando i vostri genitori sono fuori casa e provvedete a pulire il tutto. Basta un panno bagnato, l’impasto si scioglie velocemente in acqua ed ovviamente non è tossico, anche se sconsiglio di ingerirlo, chissà che non parta a fare quanto visto durante la peristalsi!

A breve includerò anche il video che ho realizzato!

Stay tuned!

Puoi leggere l\’Articolo completo direttamente sul sito di Carlo Nicolini

Page 6 of 7

« 1 … 4 5 6 7 »